Derivatives

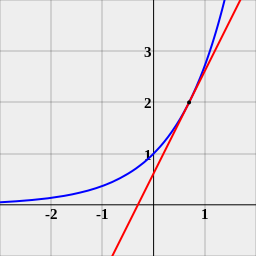
So we introduced the term derivative. A derivative is the exact value for the instantaneous rate of change at a specific point. To calculate the derivative, you would find the slope of the tangent line. A tangent line is a line that touches our graph at only one point and "does not cross the graph". This definition was one we came up with in class, and may need revising as we gain more knowledge of tangent lines.

We decided that our class will not actually calculate the derivative of the function using calculus techniques. Instead, we will continue to use our approximation technique. Some students have discovered an easier method of using the calculator to calculate the slope of the tangent line. Maybe they will share with us....

The answers to HW14 are:
1. -96
2. anything within 1% of 2866
3. -.14

Be prepared for a quiz...Can you approximate the instantaneous rate of change of a function at a specific point? For example, what is the derivative or instantaneous rate of change for f(x) = 3x^2 + 4 when x=5?

HW14

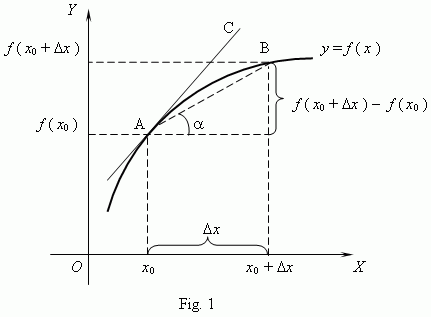
Questions, comments?

What is a Derivative?

Visit our homework site for a file that explains instantaneous rate of change.

Confused...

I was a little confused today. We were discussing HW13, which for problem #2, asked us to find the average rate at which the oil slick grew. There seemed to be some confusion about how to do problem #2. Why? When this lesson was planned, Ms. Jones and I thought there would be very little confusion about #2. Were we mistaken to in thinking that?

To us, we thought of it as just another rate of change problem, which we have done alot of examples of -- even had several rate of change problems on our 2 quizzes. Why was this one different?

That's Just The Way It Is

By now you have probably heard of some upcoming changes that will happen at Jones. How do you feel about the changes that have occurred at Jones this year? What are your feelings on the scheduled changes?

Watching this video (sorry if YouTube is blocked), there is a line..."We ain't ready, to see a black President"...any reactions?

But, How?

How does this animation relate to what we are doing in class? And if you notice that at the end of the animation, there is a f'(Xo). What do you think f'(Xo) means?

What a minute...

Today in class we were looking at the graphs of average speeds, which we called "secant lines". We agreed that to calculate the average speed, we would take the change in distance and divide it be the change in time. So we used this formula and found that our average speeds were

• 8 m/s from 0 secs to 50 secs
• 10.5 m/s from 25 secs to 50 secs
• 12 m/s from 40 secs to 50 secs

We noticed that as the average speeds increased, the slopes of the associated secant lines also increased (they got steeper).

Then we talked about finding the instantaneous speed at 50 secs. Students started mentioning strategies that sound very much like the strategy for finding average speed. They said we needed to use 2 points, and to use the average speed formula above.....

How is their strategy finding instantaneous speed? How is it any different than finding average speed? If their strategy is different, what makes it different?

We finished the class by using our calculators to zoom in on two points really close to the point, (50,400), in order to calculate the slope. Why should we care about the slope of these two points?

Average Speed VS. Instantaneous Speed

Can you compare and contrast "average speed" and "instantaneous speed"?

These sites might help...
http://mathworld.wolfram.com/SecantLine.html
http://en.wikipedia.org/wiki/Image:Derivative.png
http://www.ies.co.jp/math/java/calc/limsec/limsec.html
http://www.math.umn.edu/~garrett/qy/Secant.html
http://www.glenbrook.k12.il.us/GBSSCI/PHYS/mmedia/kinema/trip.html
http://library.thinkquest.org/C0110840/instant.htm

Questions, comments?

POW 9 solutions...

Today we went over different solutions to POW9.

The formula to calculate the height of the tallest platform:
ht = hi + d(n-1), where "ht" is the height of the tallest, "hi" is the height of the initial platform, "d" is the difference in height between the platforms, "n" is the total number of platforms.
Can you explain how this formula works?

One method to find the amount of fabric need for all of the platforms is to add up the height of each platform.

Fabric = hi + [hi + 1d] + [hi + 2d] + [hi + 3d] + ... + [hi + (n-1)d]
Notice that the last term, hi + (n-1)d, is actually hf, the height of the final platform.

But some people mentioned that adding up all of the heights is not an instant way to get amount of fabric. Plus, you kind of need to know the number of platforms to figure out how many times you have to add the numbers.

One formula that we could use to instantly calculate the amount of fabric need for all of the platforms:
Fabric = n(hi + hf)/2
Can you explain how this formula works?

See 3 very good examples of my POW journaling expectations. Example 1. Example 2. Example 3.

HW11

Today in class we were discussing HW11. Some classes didn't get an opportunity completely go over problem 5. Here are some student responses problem 5. Unfortunately, we have conflicting answers...so what do we do now?

Also, some students were not able to get to the BIG DOG problems from today's quiz. If you want to look at them here they are.

Formative Quiz 2

Questions, comments, suggestions?

Finding equations given...

Today in class we talked about HW9.

For Part I problems, we were given the slope and a point on the line. Then we then had to find the equation for the line. Can you do this? If you need a refresher, visit this site. Here is a worksheet if you would like extra practice.

For Part II problems, we were given two points on a line. Then we then had to find the equation for the line. Can you do this? If you need a refresher, visit this site. Here is a worksheet if you would like extra practice.

In some of our classes today, the point-slope form of linear equations was brought up. If you would like to know more about point-slope form, visit this site.

We then examined strategies to determine if two lines were parallel. Are these equations parallel?

• 2x + 4y = 12
• 4x + 8y = 16

SAT?

Some students and parents asked for some advice on the upcoming SAT test. Below are some links that I found -- I am not endorsing any of them, but just want to provide some links. Its also interesting to know that, "Most students are surprised to find out just how basic SAT math is: arithmetic, geometry, algebra, and a smattering of elementary logic and probability".

http://school.familyeducation.com/college-prep/sat/39916.html
http://www.collegeboard.com/student/testing/sat/prep_one/multi_choice/pracStart.html
http://www.collegeboard.com/student/testing/sat/prep_one/spr/pracStart.html
http://math.rice.edu/~lanius/Geom/quiza.html
http://www.algebra.com/testing/scripts/st.mpl
http://www.dekalb.k12.ga.us/instruction/sat/files/ECAE4D47913141C3AF95F8D76D39E409.pdf

I would recommend taking several practice tests from some of the SAT prep books.
If you have any questions about specific problems, I will definitely be willing to discuss them with you.

Back to School Night

I want to thank everyone that came to our Back to School Night. I hope that we can work together to develop mathematical thinking in our students. Links to copies of documents that were available during the sessions are below.

Again, I want to invite you to visit our class while we are discussing mathematics -- the door is always open.

Here is the syllabus for our class.
Here is the homework policy that the Math Department is implementing this school year.
Here is the document describing how you can help your child with their math homework.
These are also questions that you can ask your child about their work.
Here are the learning outcomes for our first unit, "Small World, Isn't It?"

POW9

The expectation is that you spend 10 minutes a night working on the POW. We want you to journal your work each night. Write down your goals, strategies, diagrams, charts, and your work in your journal. At the end of each session, write a reflection on what you discovered and what remains to be done to solve the POW. Your journaling of POW9 and the solution is due Monday, September 22.

Kevin is definately a slacker.

If you have any questions about the POW, add a comment.

Quiz 1: Rate of Change

Each question was worth 4 points and scored as follows:

• 4 pts : (Complete Understanding) A correct solution and an appropriate stategy were shown and explained.


• 3 pts : (Nearly Complete Understanding) A complete, appriopriate strategy is shown or explained but an incorrect solution is given due to a simple computational error - or - no solution is given - or - a correct solution is given with no strategy or explanation.


• 2 pts : (Understanding of Some of the Outcome/Concept) Some parts of an appropriate strategy are shown or explained, but some key elements are missing - or - some parts of the strategy is inappropriate - or - strategy was implemented incorrectly.


• 1 pt : (Very Little Understanding of the Outcome/Concept) Some work or explanation beyond re-copying data, but work would not lead to a correct solution.


• 0 pts : (No Evidence of Understanding of the Outcome/Concept) No work or solution shown or explained - or - some data from the problem is copied over but no evidence of any strategy is shown or explained.

The grading scale for Quiz 1 is:

• A : 14 - 16


• B : 12 - 13


• C : 8 - 11


• D : 6 - 7

I record Big Dog problems in my grade book, but those problems do not count for extra points on the quiz. Instead, they will be used as evidence that you understand a particular outcome/concept. They will also be used at the end of the semester. If your grade is on the border of the next higher grade, Big Dog problems can boost your score up to the higher grade.

The Answers to Quiz 1 Big Dogs are:

1. 21 m


2. .114 m/s


3. Anything between 7.5 - 15 secs


4. .75


5. y = (5/6)x + (10/3)

Slope and Slant

Tonight's HW is HW8.

In class today we worked on "Slope and Slant". We talked about the relationship between the slope of a line and the angle of inclination of a line. Here are some websites that talk about today's topic.

http://www.mathwords.com/a/angle_inclination.htm
http://en.wikipedia.org/wiki/Grade_(slope)
http://math.about.com/library/weekly/aa120502a.htm

How does the slope relate to the angle of inclination?

"As the slope of the line gets steeper, then the angle of inclination......."

What general principle (using trigonometry) relates the slope of a line to its angle of inclination?

Bored?

Here are some copies of Final Exams from various math courses at Southern Illinois University.

Math 107 -- Intermediate Algebra
Math 108 -- College Algebra
Math 111 -- Precalculus

Are there any problems from the Math 107 final that we should talk about?

#18 relates to what we are currently doing. #30, 32, and 33 are good ones as well. For #33, what dimensions would create a box with the largest volume?

I also like #27 from the College Algebra final.

Solving for Slope

The other day we worked on the worksheet, "Solving for Slope". You were given linear equations in Standard Form (Ax + By = C) and asked to convert the equations into Slope-Intercept Form and to determine the slope.

Here is an interactive website that shows you the steps to convert Standard Form linear equations.
http://faculty.ivytech.edu/~wmiley/Stand2Slope/StandToSlope.html

Here is a video demonstration by a teacher converting a Standard Form equation.
http://revver.com/video/521094/converting-to-slope-intercept-form-and-graphing/

Here is a video for those that would like to review Slope-Intercept Form.
http://revver.com/video/248264/slope-intercept-form/

"Solving for Slope" asked some interesting questions regarding the general equation Ax + By = C

• How could you tell if the line is has a positive or negative slope just by looking at A, B, and C?
• How could you tell if the line has a positive slope and is steeper than y = x just by looking at A, B, and C?
• How could you tell if the line has a negative slope and is steeper than y = -x just by looking at A, B, and C?

And finally, could you convert the other way around -- given an equation in Slope-Intercept Form, convert it into Standard-Form?

Help with Engineering Supplies

Help....I need somebody....Help....Not just anybody....

My engineering class is building mousetrap cars and we need your help. If you have toy cars that you don't play with anymore, old CD's, an extra dremel, or your father's drill that you can sneak out in the morning sun, then could you think about donating them to our class? We are in need of supplies to complete our cars. Visit here to see the list. Maybe we could put your name on the hood of our cars as sponsors?

How do you feel about the class?

Now that its been two weeks, how do you feel about the class? Hate it, love it, still can't tell?

Formative Quiz 1

Okay, so we had our first quiz. It was a formative quiz, meaning that it was for feedback and not for a score. We had an opportunity to discuss the results of the quiz with our group. Tomorrow, we will have a summative quiz, which is for a score.

What concerns, questions, or comments do you have about the formative quiz?

Do you think the results of the formative quiz will help you to perform well on the summative quiz?

Was the feedback you got from me effective? Were you able to understand what you needed to do?

Out of curiousity, do other teachers also give formative/practice quizzes?

Average rate of change

Is the average rate of change for the green function from 0 to 12 the same as the average rate of change for the red function from 0 to 12?

That was part of our discussion during today's class...does the average rate of change vary if the endpoints remain the same?

We then were able to rediscover the "forumla" for the slope of a line given two points.

Finally, we were able to find the slope of linear equations in Standard Form.

Any comments, questions, or observations from today's class?

How fast?

Today in class we worked on this warmup problem:
Calculate the average speed if you travel

1. one hour for 10mph and one hour for 20mph


2. one hour for 10mph and two hours for 20mph
   

We discovered that we could not just add (10+20) and divide by 3 hours for the second problem. But that we have to take into consideration the number of hours we traveled at each speed. Someone mentioned that we had to take a "weighted average". Another student mentioned that we had to calculate the "total distance traveled" and divide that by the "total elapsed time ".

Are these three strategies the same? Is one better than the others? Is one easier than the others? Is one more efficient than the others?

We then talked about ways that Ms. Jones and I could grade problem number 3 from HW4. We decided that:

• the total distance traveled has to be 550 miles


• the total elasped time has to be 11 hours

A couple of classes added this requirement as well: "the average speed has to be 50mph"

Do we "need" the last item? Will these items hold true for every valid scenario? Does it hold true for your scenario?

HW4

Add a comment and share your answers to HW4.

Do you agree with the answers already posted?

What questions do you have about HW4?

What questions do you have about your fellow students' answers?

What difficulties did you encounter with this homework?

HW3

We passed out the packets for Small World, Isnt it. There are still some extra copies left if you need one.

In class today we talked about the avg rate of change and how it related to slope. Many of you remembered slope, saying its the "rise over run" and could recite the formula for slope. Is slope the same thing as "rate of change"?

Our objective sheet for Rate of Change lists:

• Evaluate the average rate of change given points on a graph.


• Understand the relationship between the rate of change and the appearance of its graph.

Can you accomplish those goals? If not, can you write a question in the comments section that is related to where you are having difficulty with?

Tonight's homework is HW4.

How many more people?

Today's objective/outcome was to look at Rate of Change. You can view all of the outcomes for the Small World unit by looking at the learning outcomes document.

From HW2, some students mentioned that from ages 3 to 6, there was a "steady" increase in the boys' heights (problem #2). Other people mentioned the words "linear", "constant growth", "consistant growth", and "slope".

We then looked at the population graphs from Thursdays. We were able to calculate the average increase in population per year. Can you do this?

Does this "average increase in population per year" relate to "rate of change"?

Do you have any comments, suggestions, or concerns about the class so far? If so, add a comment to this post.

Homework due Monday is HW3. Our grace period is up. I will start enforcing the homework policy, the tardy policy, and the ID policy.

Total land surface area

Our book is defining "squashed up" to be 1 square foot of space per person. Personally, I feel like that is way to close to get to someone. However, using that definition, we calculated that the population of a "squashed up" earth would be 1.6x10^15 people or 1.6 quadrillion people. That's alot of people.

We talked about using scientific notation to help us look at very big numbers, like a sextillion or a quattuordecillion.

Visit the JCP homework site for HW2.

Small World, Isn't it?

Today we talked about our unit problem, Small World, Isn't It?

Our goal is to figure out how long it will take for the world's population to grow to the point that we are all "squashed up" against one another.

We talked about some factors that can affect population growth including: food sources, natural resources, disease, climate, birth rates and death rates.

Some groups came up with strategies on how to solve this problem, but seemed to run into difficulties.

What difficulties did we talk about? Issues? Things that need to be clarified?

Homework tonight is HW1.

first day jitters...

After getting off to an alarming start, I think our classes went well.

Any comments on the "Fair, but not equal" statement?

How should mathematicians define "crowded"?

And finally, any comments on the parachute activity?