Pythagorean Properties for Trigonometry

This page has a bunch of trigonometric properties.

This site derives the different pythagorean properties.
Here is trig property matching site.

Its SNOWING...

I stumbled upon this blog. I thought it was interesting. It looks like this class is doing pretty much the samething we are doing. Notice this post about the Pythagorean Property. I also like the idea of having students as scribes to blog about what happened in class each day. I am definately going to think about incorporating that into the class.

Here is another math blog. A. B.

Polar Coordinates

Here is an example of polar graph paper. Notice that its circles of different sizes.

What would the polar coordinates be for the point indicated on this graph?


I would estimate (4, 48 degrees).

Here is the wikipedia entry for polar coordinates.

This website might help. Here is another.

Here is a java script that is pretty good.

NO.NO.NO.NO.

The Physics teachers (thanks Mr. Lin and Ms. Kovacs) said that we are not done with HighDive. They said that it's okay to neglect the wind resistance, to neglect the "mass" of the diver, to neglect the friction in the bearing of the Ferris wheel, to neglect the fact that we would need Hulk Hogan to hold the diver by his legs, and to neglect the unlikeliness of a diver being able to actually dive into the cart and not SMASH his face on the bottom of it.

BUT, there were adamantly against us not taking the initial velocity of the diver into account.

What do they mean by the "initial velocity" of the diver?

Quiz

Friday we will have a quiz that will address Goals 1 and 2.

1. Graph trigonometric functions and variations on those functions (and be able to identify the critical points)


2. Relate the concept of inverse functions to define inverse trigonometric functions (and be able to find missing angles)

How comfortable are you in regards to these 2 goals?

This is a pretty good study guide. Here is another one.

Here is a good site to see how changing values affects the amplitude, period, and the midline.

What is a sine equation that represents this graph?

Cool Physics Pics

These are some cool pictures. But, do they relate at all to our High Dive Unit problem?

Almost Done?

I think we have learned enough to solve the unit problem.

We have equations to calculate the height of the diver, the x-coordinate of the diver, the fall time of the diver, and the x-coordinate of the cart.

We tried to see if the diver would fall into the cart if the wheel time (W) was 13.33, and we discovered that the cart would pass the diver.

On our group quiz, we tried to see if a wheel time (W) of 9.5 would work, and from examining the quizzes, most groups are saying that "NO" the diver will not fall into the cart.

What strategies could we use to solve for the "right" W?

Equations...

Today in class we generated several equations.


Which ones were helpful? Which ones should we definately have in our notebooks? Which ones should be taped to the wall of our classroom?

One equation we discovered was for fall time -- and I don't mean autumn. Can you use your calculator to calculate the correct fall time if I give you a "wheel time" of 22 seconds?

Ferris wheel videos

Not me...


Interesting...


Can we rent this for Fun Fair?


This looks amazing, but I would have to close my eyes...


We should bring this guy to Navy Pier with us...

FreeFall

Answers are posted on the Homework Site.

It looks like the mass of an object doesn't affect the time it takes that object to free fall. Does that make sense? A grape and a bowling ball dropped from the same height will take the same amount of time to fall to the ground?

Any questions, comments, or suggestions?

Check out this video.

HW8

What was the point of HW8?

Isn't average speed just the average (mean) of the inital speed and the final speed?

What's the average speed of this graph (from 0 secs to 20 secs)?

HW7 Part 2

How do we solve these problems from HW7 Part 2?

• How do we find 3 values of θ, other than 15°, such that sin θ = sin 15°?
• How do we find 3 values of θ, such that sin θ = -(sin 60°)?
• How do we find 3 values of θ, such that sin θ = 0.5?
• How do we find 3 values of θ, such that sin θ = -0.71?

What strategies can we use?

Check this link out. Here is the beginning of the unit.


Here is a quiz to test your understanding.

What Should We Do?

There are some CRAZY people out there....

Last week, the Math Department went to a dinner at DePaul University to celebrate our Research Lesson Study. I got some really good feedback from people that attended our lesson. They were really impressed by the group conversations that happened during the lesson. Several commented on how you (the students) were able to discuss different answers and decide which ones met the criteria and which ones didn't meet the criteria. Ms. Fulton and Mr. Bywater are planning on re-doing the lesson in March, infront of an even bigger audience. I saw pictures of the lesson, but they are still working on the video.

While at the dinner, I mentioned about our class wanting to rent out the Ferris wheel at Navy Pier. One of the dinner hosts was really excited about that, and has promised to make some phone calls. Hopefully, he is able to excite some more people.

Ms. Jones will be finishing up her Student Teaching soon. I think her last day is in 2 weeks, but I will have to double check. What should we do, if anything? Ideas? Suggestions?

Ocean Tide

Today we talked about Shelly and her sandcastles.

Here is the Sand Sculpture Capital of the World.

How do you think they made this?

This one reminds of me of my daughter's book, "Hands, hands, fingers, thumb...one thumb, one thumb, drumming on a drum".

Now this is cool. How big do you think it is?

Back to our work....

To solve #4 from HW6, we discussed several strategies. We said we could use the "trace" function on the calculator. That worked pretty well. Then someone discussed how we could use the table on the calculator. This gave us more precise numbers, especially when we changed the increments on the table. A third strategy was to graph the equation y = -10 and use the "calculate" function to find the intersection points. This would definately give us the correct answer.

How could we do this algebraically?

Amplitude and Period

Today in class we talked about amplitude and period.

How would you define amplitude?
How would you define period?

Can you identify the amplitude and period from the graph below? (Note π is 180° and 2π is 360°) Eventhough we haven't studied this specific graph, can you create an equation using sine that will give you this graph?

Can you determine the amplitude and period just by looking at the equation? For instance, in the equation y = 12 sin (4x), what is the amplitude? What is the period?

Periodic Function

We are currently studying Periodic Functions.

Below are some examples of periodic motion that we could examine mathematically and find their periodic function.






Can you identify other examples of periodic motion? Add a comment and share your examples.

Cool Ferris Wheel Animation

Visit here for a cool Ferris wheel animation.

Is anyone familiar with Geometer's Sketchpad? Here is a Ferris wheel creation.

Can you solve this problem?

Goals Check-In

I want you to reflect on our goals for the High Dive Unit.

What goals have we address so far in class?
What assignments helped you develop those goals?
How confident are you in demonstrating evidence that you are a master of those goals?

Our Equation

Does our equation to find the height off the ground of the cart of the Ferris wheel always work?

h(t) = 65 + 50 sin (9t)

In class today we examined the sine of "large" angles and compared them to the sine of their reference angles. What did we discover? How does that discovery affect our height equation? Can we always trust our height equation, or do we need to know what quadrant our cart is in before we trust the height equation?

Inverse Trig Functions...

We used inverse sine today in class to solve our HW3. What is "inverse sine"? How does it work? As a student, can I just skip it and hope we don't have some big old quiz with tons of inverse sine questions?

Right Triangle Trigonometry

Need a refresher in Right Triangle Trig? Forgot how sine, cosine, and tangent work?
Watch these YouTube videos.
Here. Here. Here. Here.


Want more practice?
Visit these sites for more practice.
Here. Here. Here. Here.

HW3

Any questions?

HW2

Today we looked at our Unit Ferris wheel. What were some key facts about the Ferris wheel?

Visit our homework site for the answers to HW2.

Can you get those same answers? If you are having trouble, post a question.

What important ideas do we need to solve HW2?

Finding the height

Today in class we talked about how to find the height off of the ground of Al and Betty as they ride around the Ferris wheel.

Can someone post a comment to restate how we can find the height? What important mathematical concept do we need to find the height? Are there different positions on the Ferris wheel that are at the same height?

How would you calculate the height of a person if they were positioned at 1:30 (in between 1 o'clock and 2 o'clock)?

Can you generalize a procedure to find the height at any position? What information would you need?

Here is a link that might help.

HW1

We should go visit Santa Monica's boardwalk. Now that's a cool looking Ferris wheel.

How are you doing on HW1? Any difficulties? Leave a comment.

POW1

How is POW1 going?

Is it possible for the monks to accomplish this task?

Anyone having difficulties?

Leave a comment.

High Dive

We are finally done with Small World. Hurray!

Next up is the High Dive Unit. The High Dive is the first unit from our IMP4 book. Some students have an IMP4 book already. If you did not get a book, you will get pick it up on Wednesday.

Has anyone read the book, The Devil in the White City? I heard its really good. Its set in Chicago during the World's Fair in 1893. During that World's Fair, George Washington Gale Ferris debuted the Ferris wheel. While in the planning stages, fair organizers thought that Ferris was a lunatic and was dubbed "The Man with Wheels in his Head."

The World's Fair Ferris wheel was built on the Midway Plaisance, by the University of Chicago. This was no ordinary Ferris wheel.

From The Alleghenian newspaper: "It is almost impossible either by picture or description in words to give you an idea of what this wheel is like. A mere statement of its dimensions, 250 feet in diameter, 825 feet in circumference, 30 feet broad and weight more than 4,000 tons, does not mean much to the average mind. It may help the reader to understand what the structure is like if I say that the highest point of the wheel is as far from the ground as the top of one ten-story building would be if it were put on the roof of another building of equal height...There are thirty-six cars on the wheel. Each is 27 feet long, 9 feet high and 13 feet broad. .. Each car will seat, on revolving chairs, forty passengers. Therefore the thirty-six cars will seat 1,440 passengers. But with standing room occupied the wheel has a capacity of 2,000 persons."

Here and here are a couple of more links describing the Ferris wheel.

Assessment and Portfolio Moved to Thursday

Both the Small World Unit Assessment and Portfolio will be due on Thursday. Tomorrow will be another day for review, peer editing, and working on your portfolio.

Enjoy this historical night.

Move Small World Unit Assessment to Thursday?

Grades are now due Friday. Because of this, I am willing to move our Unit Assessment to Thursday. Is that okay? How do you feel about moving the date of the assessment?

Leave a comment to voice your opinion regarding moving the assessment from Wed to Thursday.

I will use the comments to make my decision -- contact your classmates and tell them to leave a comment.

More on the portfolio & assessment

Reminder: You can ONLY use the portfolio on the unit assessment. Your Appendix section has no page limit.

Here are the solutions to Quiz 6.
Here is a copy of the study guide we passed out today.
And finally, here are solutions to the study guide.

The Other Grammy's

It was a wonderful show last night. I was really impressed with all of the acts. Its a beautiful thing seeing students outside of class.

Mr. Bywater did a piece on The Roots. Here are some cuts off of their first commercial release, "Do You Want More?"
http://www.youtube.com/watch?v=cPepJ43SqJY&feature=related
http://www.youtube.com/watch?v=AAqVHnsLww0&feature=related

Ms. Moody did a tribute to Tribe Called Quest.
http://www.youtube.com/watch?v=kpPkGZ6zhzA
http://www.youtube.com/watch?v=9z11Dqw7mK0

But, we can't really talk about The Roots or Tribe without mentioning these...
http://www.youtube.com/watch?v=WQzoDd5_im8
http://www.youtube.com/watch?v=AmKNRNGvZu0
http://www.youtube.com/watch?v=Zu4RM1Iq-wg
http://www.youtube.com/watch?v=CfrNF9GOMUs
http://www.youtube.com/watch?v=v5BZom3vY0g
and this list could go on and on....

What's interesting to me is that people are always talking about the "good old times"...
"I remember when hip hop was" blah blah blah. We didn't have this and this...It used to be more than just a dope beats with no lyrics...more than just a catchy hook...more than just something to dance to...But wait..."old schools" did have these...
http://www.youtube.com/watch?v=_Ahle1zq6NQ
http://www.youtube.com/watch?v=BaeNelsAOGo
http://www.youtube.com/watch?v=7iSfuaPDcTc
http://www.youtube.com/watch?v=Vp-is6S_b_g
http://www.youtube.com/watch?v=DcNUx0-XEfw
http://www.youtube.com/watch?v=BnrLloO7nFQ
http://www.youtube.com/watch?v=Jbxi9hxctk8

"Small World" Portfolio and Unit Assessment

Any questions about the portfolio? The unit assessment?

Here are the requirements and the rubric for the unit portfolio.

Here is a pdf of supplemental materials from a Precalculus course at Arkansas Tech University. Sections 1-20 are all applicable to our Small World Unit.
For Example:

• Page 11 has examples on Rate of Change
• Page 15 discusses Linear Functions
• Page 18 goes into formulas of Linear Functions
• Page 30 show how to find the Inputs and Outputs of Functions
• Page 51 discusses Exponential Functions
• Page 55 compares Exponential Functions and Linear Functions

If you want to "read" the book that the Arkansas Tech University Precalc class uses, here is a preview. If you want to actually buy this book, buy it used from a used textbook site like alibris. I think it is a really good reference book.

Here is anther pdf comparing Expnential and Linear Functions.

Strategies for solving Small World Unit Problem

Yesterday we said the general form for exponential functions is:

Today in class we discussed several strategies to help us solve our Unit Problem for Small World.

Recall that we need to find out when the population will reach the point that we are all "squashed up". Earlier we said that this will happen when our population reaches 1.6x10^15 people. We decided that population growth was best modeled by an exponential function.

What strategies did we discuss?

1. One was to input our data from the tables into the calculator. Here is a sheet of instructions to enter data into the calculator. Then we could guess equations that fit our data the best -- like "Tweaking this Function".





2. Another way was to do something similar to HW25 and HW29. Use two of the data points and solve for the variables k and c. Some people said that in order for this strategy to work, we would have to set one of our years to 0, just like HW25 and HW29.





3. An even different approach is to use the calculator's regression feature. I am not advocating this approach, but it is a valid approach. However, you may need to do some calculations to convert the equation into the form we want the final answer to be in.

Ok.Ok.Ok. Say we use one of those strategies. And say we get an exponential equation that models our data really well. Then what? Are we done? Have we solved the unit problem?

Oct 28

In class today we went over HW28: The Limit of Their Generosity.

Yesterday, Adam deposited $1000 in the bank. At first the bank was going to double his money in 20 years.

Adam persuaded the bank to instead of giving him 100% interest at the end of 20 years to give him 5% interest each year for 20 years.

Adam them persuaded the bank to calculate the interest every 6 months and then persuaded them to calculate the interest every 3 months.

Adam noticed that he was getting more money the more often the bank was calculating the interest.

In HW28, Adam tries to persuade the bank to calculate the interest on a daily basis and then on an hourly basis. In class we even calculated on a minute basis.

What discoveries did we make? Please share your results (several students were absent from class b/c of PSAE testing and would benefit from sharing results).

Lastly, we tried to solve this equation: 2^x = e^?
Can you find the value of the question mark?

History of e

Today in class some questions about the history of e came up.

Here is link that descibes how e came about and several different ways to determine the value of e.

Here is another link about e.

And That is Why I Succeed

One of my favorite commercials



Air Jordan Air Jordan Air Jordan


Do you know Do you know Do you know


Maybe...

Small World Portfolio

We are a couple of days away from finishing our Small World Unit. With that, we will have a Unit Assessment and we will create a Unit Portfolio.

Remember this sheet I passed out at the beginning of the unit?

Well, now is a good time to go through the sheet and identify homework assignments, classwork assignments, and quiz questions that relate to the outcomes/goals.

For your portfolio, you will be required to select either a homework or classwork for each outcome/goal of the unit. The assignment that you select for the goal must have a fully explained and correct solution. It doesn't matter how well you understood the assignment at the time it was assigned. Now is your opportunity to demonstrate what you currently understand.

More specific information about the portfolio will be given in class in the near future.

Leave a comment to compare your opinions about some of the assignments and their learning outcomes.

Compound Interest

Today in class we discussed compound interest. Would anyone like to share their general formula?




If you were Adam, how would you want the bank to calculate your interest? Yearly? Quarterly? Daily? Instantly?




We then looked at the supplemental problem -- trying to figure out the percentage rate that will exactly double Adam's money in 20 years. How do we solve this?




Some classes got 3.526% by guess and check...How else could we solve this? Scroll down if you want to know.....

CLEP Precalculus Exam

Here are some sample problems for the CLEP Precalculus Exam.

Look at problems 7, 9, and 10 -- logarithms.

UIUC Engineering OPEN HOUSE

Would anyone like to attend the Engineering Open House at UIUC?
Watch this video from the 2007 open house.

Thank you for your support

The Jones Math Department wants to thank everyone that participated in our Research Lesson. This summer our department joined the Lesson Study Group. We worked collaboratively on the research lesson and invited guests from across the city to come observe the lesson and give our department feedback on the lesson.

We got some really good feedback -- things that were well done in the lesson, things that were confusing about the lesson, and things that were not done well in the lesson. Even though it "hurts" to receive candid feedback, we are excited by it, as it will improve our instruction.

The volunteers should be very proud of themselves. The observers were very impressed by the way your groups were able to evaluate the different graphs and determine which graphs met the criteria and which graphs did not meet the criteria. They mentioned that typically teachers hold the authority in class -- that teachers validate correct answers to students. But in this lesson, students were the authority and validated the correct answers. The observers also made several comments on how well groups worked collaboratively by sharing and discussing ideas.

Again, the math department cannot thank you enough for your participation in our research lesson.

SPECIAL THANKS TO:
Tom McDougal
Dr. Takahashi
Dr. Powers
Margie Pligge
Salik Mukarram
The Jones staff
Edwardo's

Progress Reports.

Today we passed out updated progress reports. The report can be alittle confusing.

The top portion is what is used to calculate your grade. It looks like you have taken about 16 quizzes but, each entry is actually one problem on a quiz. Quiz2.3 is really question #3 from Quiz 2. We entered the information this way so that we could generate the bottom portion.

The bottom portion is not used for calculating the grade, but to provide feedback to you. It lists all of the goals that we have studied so far. You can see which topics you could improve in. Those are topics that you may choose to review and re-assess. The calculations are not averages, but they are calculated using a power formula.

Any other questions about the progress report?

Quiz 5 Content

Can you....

*find the derivative of a function at specific points?
*graph a derivative of a function given certain conditions about the function?
*develop and use a formula for calculating interest?
*apply the principles of logarithms?

Questions, comments, or issues -- leave a comment.

The Graph of the Derivative

We have spent the last couple of days looking at the graph of the derivative.

Here is a cool applet.

This video also talks about some of the things we have covered in class.


On a side note...what would you do if this was your prom?

Quiz 4 Comments...

Any comments, questions, or concerns about Quiz 4?

If you feel that Quiz 4 didn't truely show your knowledge on the learning goals, please come see me or Ms. Jones before or after school. We can give you additional opportunities to provide evidence that you understand the goals.

The Math Department needs volunteers to star in an International Video! Imagine being seen by millions, billions, ALOT of people.

What? Where? When? You will have to come to school on Friday, October 24th from 9:00 am to 11:00 am. We will provide you with breakfast and lunch. You will have your own "green room" to prepare for your video shoot. Unfortunately, we won't be able to accommodate performer riders, but we can meet some dietary requests.

Why? Mr. Bywater, Ms. Fulton, Mr. Remiasz and I participated in a workshop this summer to improve our teaching, which ultimately improves student learning. We designed a math lesson that we want feedback on. Math teachers from different schools will observe and critic the lesson. We will gain valuable information from having these experts analyze and evaluate our performance. This lesson will have a tremendous effect on our practices and will help establish the Jones College Prep Math Department as a well respected, research-leading department.

I want to thank those individuals that volunteer, in advance. Words cannot express our thanks, appreciation, and gratitude for your committement to helping the Jones College Prep Math Department grow and improve.

HW24

The answers to HW 24 were....

1.a.i. $10,500

1.a.ii. $2521.05

1.a.iii. $423.71

1.b. V(t) = 15000 ( 1 - .30 ) ^t = 15000 (.7) ^t , where t is the number of years after 1990.

2. Clarabell is wrong. The more expensive car will NEVER be worth less than the cheaper car. We verified this by looking at the graph of the two equations, looking at the table of the two equations, and by trying to find the intersection of the two equations.

Exponential Functions

Recently, we've been talking about exponential functions. We examined various exponential functions to determine which ones have the "proportionality property".

How did we determine if an equation had the proportionality property? What did we have to do?

We finally came to the conclusion that functions in the following form would have characteristics of the proportionality property:

f ( x ) = AB ^cx

where A, B and C are constants

This happens to be the general form for exponential functions.

Do you think there are limitations on the values of A, B, or C? Can they be decimals? Negative numbers? Equal to zero? Here is an applet that could help you answer these questions -- be patient, it takes a while to load.

Since we are examining exponential functions, here is a great tutorial and goes really well with "A Basis For Disguise", the classwork that we worked on Friday.

7 ^x= 5 ^?

Can you write a general rule for writing 7 ^x as a power of 5?

Here are some YouTube videos demonstrating how to solve exponential equations.

POW10: Around King Arthur's Table

Questions or comments? Do you have an answer? What have you tried? What doesn't work?

HW20

We came up with the equation for the derivatives of two functions:
f(x) = 3x + 4
g(x) = x^2 - 9

For the f(x) function, we found that the derivative is always 3, no matter what value of x we used.
Some classes developed a conjecture for all linear equations...For ALL linear equations, the derivative IS the slope.

For the g(x) function, we found that the equation for the derivative is 2x, and changes depending on the value of x.
One class developed this conjecture for all quadratic equations...For ALL quadratic equations, the derivative = 2*A*x, where A is the coefficient of the x^2 term.

NOTE: These are conjectures, which we will accept to be true until someone can find an example where it doesn't work. Can you find an example that will prove our conjecture to be false?

Slippery Slopes

For this assignment, we had to find the derivative for the equation y = 2^x, an exponential function. Most students used the "find the slope of a secant for two very close points" method. Other students use the calculator to get the derivatives. Can you do both methods?

We then tried to examine the relationship between the y-value and the derivative. Some noticed some interesting patterns -- the y-values double and the derivatives double. What makes the y-values double? For #2, the equation is y = 10^x. What patterns for the y-values did you see or would you expect to see? What patterns for the derivatives did you see or would you expect to see?

Finally, our goal was to create an equation. For 1b, some said that the equation is:

Derivative = (y / 1.44)

Some others said:

Derivative = 0.693 * y

Which is correct?

Can you create the equation for the derivative in terms of the y-value for problem #2?

Can you generalize the derivative of any exponential function (y = A^x)?

Quiz 3

Do you have any questions, comments, or concerns about Quiz 3?

Quiz Friday. Topics include all of the outcomes we have covered so far...Rate of Change, Slope and Linear Equations, and Derivatives/Instantaneous Rate of Change.

• Can you calculate the slope of a line?
• Can you find an equation of a line given two points that the line passes through?
• Can you find the slope of different secant lines of a curve/graph?
• Can you find the average rate of change given a scenario/table/graph/equation?
• Can you find the approximate instantaneous rate of change given a scenario/table/graph/equation?
• Can you find the derivative of an equation at a specific point on a curve?
• Can you draw a tangent line at a specific point on a curve?

Derivatives

So we introduced the term derivative. A derivative is the exact value for the instantaneous rate of change at a specific point. To calculate the derivative, you would find the slope of the tangent line. A tangent line is a line that touches our graph at only one point and "does not cross the graph". This definition was one we came up with in class, and may need revising as we gain more knowledge of tangent lines.

We decided that our class will not actually calculate the derivative of the function using calculus techniques. Instead, we will continue to use our approximation technique. Some students have discovered an easier method of using the calculator to calculate the slope of the tangent line. Maybe they will share with us....

The answers to HW14 are:
1. -96
2. anything within 1% of 2866
3. -.14

Be prepared for a quiz...Can you approximate the instantaneous rate of change of a function at a specific point? For example, what is the derivative or instantaneous rate of change for f(x) = 3x^2 + 4 when x=5?

HW14

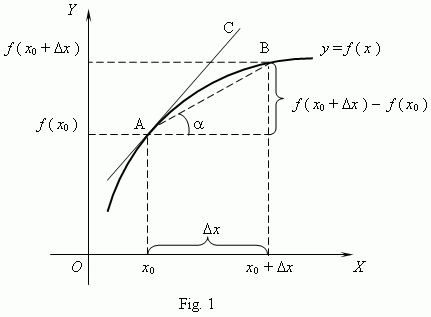
Questions, comments?

What is a Derivative?

Visit our homework site for a file that explains instantaneous rate of change.

Confused...

I was a little confused today. We were discussing HW13, which for problem #2, asked us to find the average rate at which the oil slick grew. There seemed to be some confusion about how to do problem #2. Why? When this lesson was planned, Ms. Jones and I thought there would be very little confusion about #2. Were we mistaken to in thinking that?

To us, we thought of it as just another rate of change problem, which we have done alot of examples of -- even had several rate of change problems on our 2 quizzes. Why was this one different?

That's Just The Way It Is

By now you have probably heard of some upcoming changes that will happen at Jones. How do you feel about the changes that have occurred at Jones this year? What are your feelings on the scheduled changes?

Watching this video (sorry if YouTube is blocked), there is a line..."We ain't ready, to see a black President"...any reactions?

But, How?

How does this animation relate to what we are doing in class? And if you notice that at the end of the animation, there is a f'(Xo). What do you think f'(Xo) means?

What a minute...

Today in class we were looking at the graphs of average speeds, which we called "secant lines". We agreed that to calculate the average speed, we would take the change in distance and divide it be the change in time. So we used this formula and found that our average speeds were

• 8 m/s from 0 secs to 50 secs
• 10.5 m/s from 25 secs to 50 secs
• 12 m/s from 40 secs to 50 secs

We noticed that as the average speeds increased, the slopes of the associated secant lines also increased (they got steeper).

Then we talked about finding the instantaneous speed at 50 secs. Students started mentioning strategies that sound very much like the strategy for finding average speed. They said we needed to use 2 points, and to use the average speed formula above.....

How is their strategy finding instantaneous speed? How is it any different than finding average speed? If their strategy is different, what makes it different?

We finished the class by using our calculators to zoom in on two points really close to the point, (50,400), in order to calculate the slope. Why should we care about the slope of these two points?

Average Speed VS. Instantaneous Speed

Can you compare and contrast "average speed" and "instantaneous speed"?

These sites might help...
http://mathworld.wolfram.com/SecantLine.html
http://en.wikipedia.org/wiki/Image:Derivative.png
http://www.ies.co.jp/math/java/calc/limsec/limsec.html
http://www.math.umn.edu/~garrett/qy/Secant.html
http://www.glenbrook.k12.il.us/GBSSCI/PHYS/mmedia/kinema/trip.html
http://library.thinkquest.org/C0110840/instant.htm

Questions, comments?

POW 9 solutions...

Today we went over different solutions to POW9.

The formula to calculate the height of the tallest platform:
ht = hi + d(n-1), where "ht" is the height of the tallest, "hi" is the height of the initial platform, "d" is the difference in height between the platforms, "n" is the total number of platforms.
Can you explain how this formula works?

One method to find the amount of fabric need for all of the platforms is to add up the height of each platform.

Fabric = hi + [hi + 1d] + [hi + 2d] + [hi + 3d] + ... + [hi + (n-1)d]
Notice that the last term, hi + (n-1)d, is actually hf, the height of the final platform.

But some people mentioned that adding up all of the heights is not an instant way to get amount of fabric. Plus, you kind of need to know the number of platforms to figure out how many times you have to add the numbers.

One formula that we could use to instantly calculate the amount of fabric need for all of the platforms:
Fabric = n(hi + hf)/2
Can you explain how this formula works?

See 3 very good examples of my POW journaling expectations. Example 1. Example 2. Example 3.

HW11

Today in class we were discussing HW11. Some classes didn't get an opportunity completely go over problem 5. Here are some student responses problem 5. Unfortunately, we have conflicting answers...so what do we do now?

Also, some students were not able to get to the BIG DOG problems from today's quiz. If you want to look at them here they are.

Formative Quiz 2

Questions, comments, suggestions?

Finding equations given...

Today in class we talked about HW9.

For Part I problems, we were given the slope and a point on the line. Then we then had to find the equation for the line. Can you do this? If you need a refresher, visit this site. Here is a worksheet if you would like extra practice.

For Part II problems, we were given two points on a line. Then we then had to find the equation for the line. Can you do this? If you need a refresher, visit this site. Here is a worksheet if you would like extra practice.

In some of our classes today, the point-slope form of linear equations was brought up. If you would like to know more about point-slope form, visit this site.

We then examined strategies to determine if two lines were parallel. Are these equations parallel?

• 2x + 4y = 12
• 4x + 8y = 16

SAT?

Some students and parents asked for some advice on the upcoming SAT test. Below are some links that I found -- I am not endorsing any of them, but just want to provide some links. Its also interesting to know that, "Most students are surprised to find out just how basic SAT math is: arithmetic, geometry, algebra, and a smattering of elementary logic and probability".

http://school.familyeducation.com/college-prep/sat/39916.html
http://www.collegeboard.com/student/testing/sat/prep_one/multi_choice/pracStart.html
http://www.collegeboard.com/student/testing/sat/prep_one/spr/pracStart.html
http://math.rice.edu/~lanius/Geom/quiza.html
http://www.algebra.com/testing/scripts/st.mpl
http://www.dekalb.k12.ga.us/instruction/sat/files/ECAE4D47913141C3AF95F8D76D39E409.pdf

I would recommend taking several practice tests from some of the SAT prep books.
If you have any questions about specific problems, I will definitely be willing to discuss them with you.

Back to School Night

I want to thank everyone that came to our Back to School Night. I hope that we can work together to develop mathematical thinking in our students. Links to copies of documents that were available during the sessions are below.

Again, I want to invite you to visit our class while we are discussing mathematics -- the door is always open.

Here is the syllabus for our class.
Here is the homework policy that the Math Department is implementing this school year.
Here is the document describing how you can help your child with their math homework.
These are also questions that you can ask your child about their work.
Here are the learning outcomes for our first unit, "Small World, Isn't It?"

POW9

The expectation is that you spend 10 minutes a night working on the POW. We want you to journal your work each night. Write down your goals, strategies, diagrams, charts, and your work in your journal. At the end of each session, write a reflection on what you discovered and what remains to be done to solve the POW. Your journaling of POW9 and the solution is due Monday, September 22.

Kevin is definately a slacker.

If you have any questions about the POW, add a comment.

Quiz 1: Rate of Change

Each question was worth 4 points and scored as follows:

• 4 pts : (Complete Understanding) A correct solution and an appropriate stategy were shown and explained.


• 3 pts : (Nearly Complete Understanding) A complete, appriopriate strategy is shown or explained but an incorrect solution is given due to a simple computational error - or - no solution is given - or - a correct solution is given with no strategy or explanation.


• 2 pts : (Understanding of Some of the Outcome/Concept) Some parts of an appropriate strategy are shown or explained, but some key elements are missing - or - some parts of the strategy is inappropriate - or - strategy was implemented incorrectly.


• 1 pt : (Very Little Understanding of the Outcome/Concept) Some work or explanation beyond re-copying data, but work would not lead to a correct solution.


• 0 pts : (No Evidence of Understanding of the Outcome/Concept) No work or solution shown or explained - or - some data from the problem is copied over but no evidence of any strategy is shown or explained.

The grading scale for Quiz 1 is:

• A : 14 - 16


• B : 12 - 13


• C : 8 - 11


• D : 6 - 7

I record Big Dog problems in my grade book, but those problems do not count for extra points on the quiz. Instead, they will be used as evidence that you understand a particular outcome/concept. They will also be used at the end of the semester. If your grade is on the border of the next higher grade, Big Dog problems can boost your score up to the higher grade.

The Answers to Quiz 1 Big Dogs are:

1. 21 m


2. .114 m/s


3. Anything between 7.5 - 15 secs


4. .75


5. y = (5/6)x + (10/3)