Derivatives

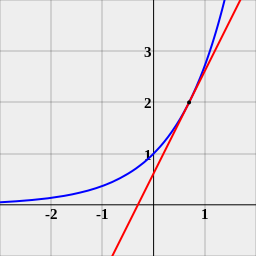
So we introduced the term derivative. A derivative is the exact value for the instantaneous rate of change at a specific point. To calculate the derivative, you would find the slope of the tangent line. A tangent line is a line that touches our graph at only one point and "does not cross the graph". This definition was one we came up with in class, and may need revising as we gain more knowledge of tangent lines.

We decided that our class will not actually calculate the derivative of the function using calculus techniques. Instead, we will continue to use our approximation technique. Some students have discovered an easier method of using the calculator to calculate the slope of the tangent line. Maybe they will share with us....

The answers to HW14 are:
1. -96
2. anything within 1% of 2866
3. -.14

Be prepared for a quiz...Can you approximate the instantaneous rate of change of a function at a specific point? For example, what is the derivative or instantaneous rate of change for f(x) = 3x^2 + 4 when x=5?